Stationary Processes, Wiener-Granger Causality, and Matrix Spectral Factorization

Granger causality has become an indispensable tool for analyzing causal relationships between time series. In this paper, we provide a detailed overview of its mathematical foundations, trace its historical development, and explore how recent computational advancements can enhance its application in various fields. We will not hesitate to present the proofs in full if they are simple and transparent. For more complex theorems on which we rely, we will provide supporting citations. We also discuss potential future directions for the method, particularly in the context of largescale data analysis.

Inferring directed spectral information flow between mixed-frequency time series

Identifying directed spectral information flow between multivariate time series is important for many applications in finance, climate, geophysics and neuroscience. Spectral Granger causality (SGC) is a prediction-based measure characterizing directed information flow at specific oscillatory frequencies. However, traditional vector autoregressive (VAR) approaches are insufficient to assess SGC when time series have mixed frequencies (MF) or are coupled by nonlinearity. Here we propose a time-frequency canonical correlation analysis approach ("MF-TFCCA") to assess the strength and driving frequency of spectral information flow. We validate the approach with intensive computer simulations on MF time series under various interaction conditions and assess statistical significance of the estimate with surrogate data. We further apply MF-TFCCA to real-life finance, climate and neuroscience data. Our analysis framework provides an exploratory and computationally efficient approach to quantify directed information flow between MF time series in the presence of complex and nonlinear interactions.

Detecting Causality in the Frequency Domain with Cross-Mapping Coherence

Understanding causal relationships within a system is crucial for uncovering its underlying mechanisms. Causal discovery methods, which facilitate the construction of such models from time-series data, hold the potential to significantly advance scientific and engineering fields. This study introduces the Cross-Mapping Coherence (CMC) method, designed to reveal causal connections in the frequency domain between time series. CMC builds upon nonlinear state-space reconstruction and extends the Convergent Cross-Mapping algorithm to the frequency domain by utilizing coherence metrics for evaluation. We tested the Cross-Mapping Coherence method using simulations of logistic maps, Lorenz systems, Kuramoto oscillators, and the Wilson-Cowan model of the visual cortex. CMC accurately identified the direction of causal connections in all simulated scenarios. When applied to the Wilson-Cowan model, CMC yielded consistent results similar to spectral Granger causality. Furthermore, CMC exhibits high sensitivity in detecting weak connections, demonstrates sample efficiency, and maintains robustness in the presence of noise. In conclusion, the capability to determine directed causal influences across different frequency bands allows CMC to provide valuable insights into the dynamics of complex, nonlinear systems.

A method to assess Granger causality, isolation and autonomy in the time and frequency domains: theory and application to cerebrovascular variability

Concepts of Granger causality (GC) and Granger autonomy (GA) are central to assess the dynamics of coupled physiologic processes. While causality measures have been already proposed and applied in time and frequency domains, measures quantifying self-dependencies are still limited to the time-domain formulation and lack of a clear spectral representation. We embed into the classical linear parametric framework for computing GC from a driver random process X to a target process Y a measure of Granger Isolation (GI) quantifying the part of the dynamics of Y not originating from X, and a new spectral measure of GA assessing frequency-specific patterns of self-dependencies in Y. The measures are illustrated in theoretical simulations and applied to time series of mean arterial pressure and cerebral blood flow velocity obtained in subjects prone to develop postural syncope and healthy controls. Simulations show that GI is complementary to GC but not trivially related to it, while GA reflects the regularity of the internal dynamics of the analyzed target process. In the application to cerebrovascular interactions, spectral GA quantified the physiological response to postural stress of slow cerebral blood flow oscillations, while spectral GC and GI detected an altered response to postural stress in subjects prone to syncope, likely related to impaired cerebral autoregulation. The new spectral measures of GI and GA are useful complements to GC for the analysis of interacting oscillatory processes, and detect physiological and pathological responses to postural stress which cannot be traced in the time domain. The assessment of causality, isolation and autonomy opens new perspectives for the analysis of coupled biological processes in both physiological and clinical investigations.

Cause-effect inference through spectral independence in linear dynamical systems: theoretical foundations

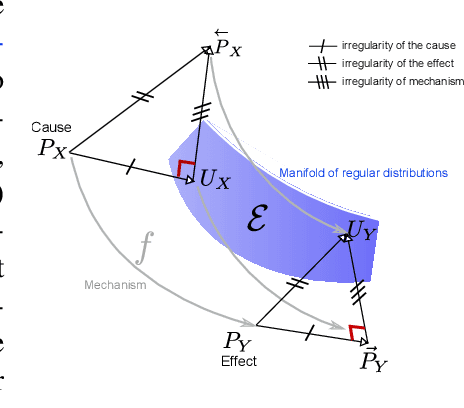
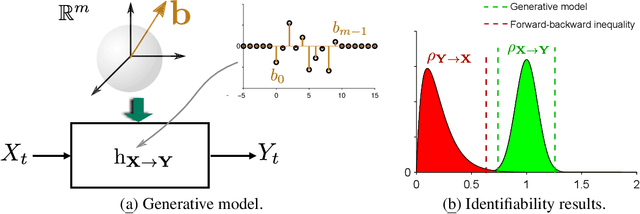
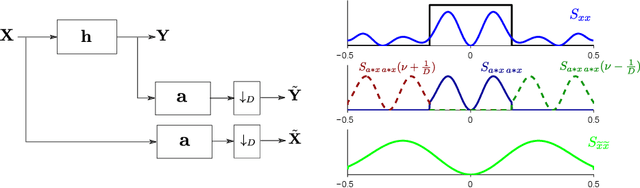
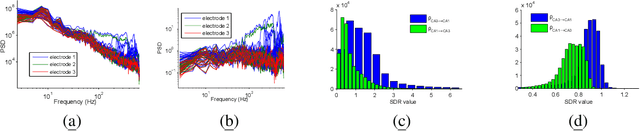
Distinguishing between cause and effect using time series observational data is a major challenge in many scientific fields. A new perspective has been provided based on the principle of Independence of Causal Mechanisms (ICM), leading to the Spectral Independence Criterion (SIC), postulating that the power spectral density (PSD) of the cause time series is uncorrelated with the squared modulus of the frequency response of the filter generating the effect. Since SIC rests on methods and assumptions in stark contrast with most causal discovery methods for time series, it raises questions regarding what theoretical grounds justify its use. In this paper, we provide answers covering several key aspects. After providing an information theoretic interpretation of SIC, we present an identifiability result that sheds light on the context for which this approach is expected to perform well. We further demonstrate the robustness of SIC to downsampling - an obstacle that can spoil Granger-based inference. Finally, an invariance perspective allows to explore the limitations of the spectral independence assumption and how to generalize it. Overall, these results support the postulate of Spectral Independence is a well grounded leading principle for causal inference based on empirical time series.

Boosted Convolutional Neural Networks for Motor Imagery EEG Decoding with Multiwavelet-based Time-Frequency Conditional Granger Causality Analysis

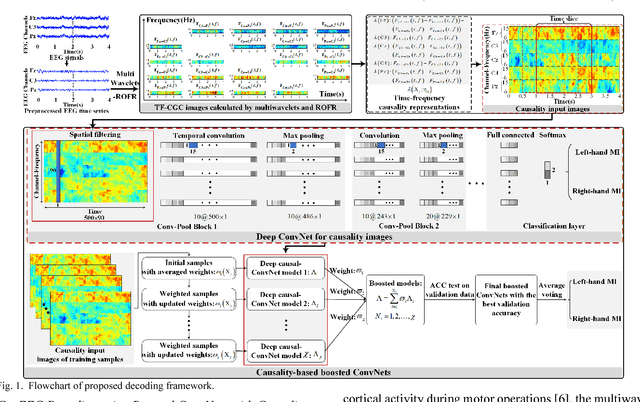
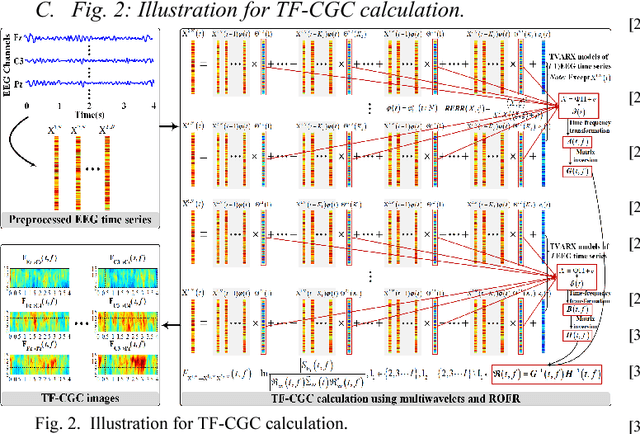
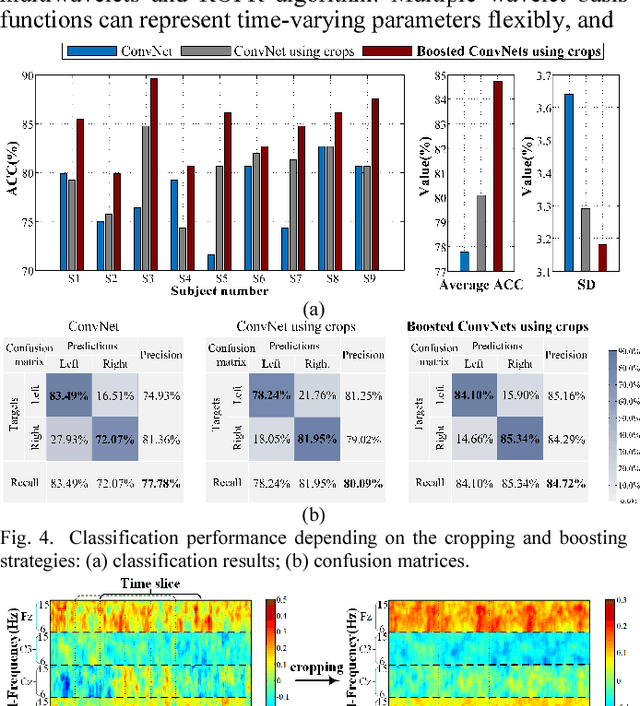
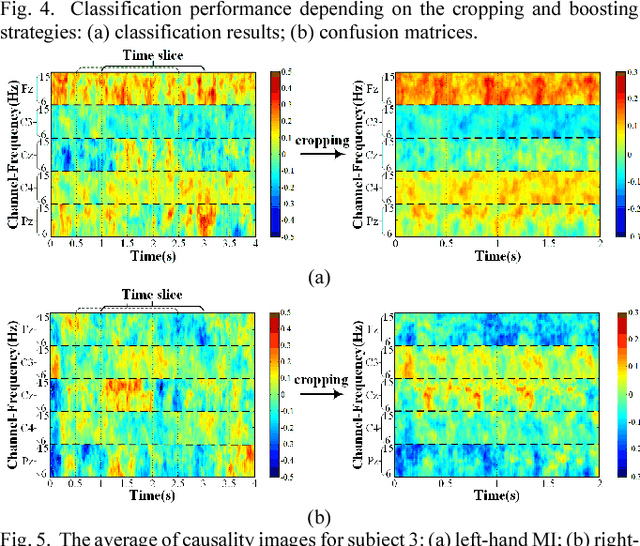
Decoding EEG signals of different mental states is a challenging task for brain-computer interfaces (BCIs) due to nonstationarity of perceptual decision processes. This paper presents a novel boosted convolutional neural networks (ConvNets) decoding scheme for motor imagery (MI) EEG signals assisted by the multiwavelet-based time-frequency (TF) causality analysis. Specifically, multiwavelet basis functions are first combined with Geweke spectral measure to obtain high-resolution TF-conditional Granger causality (CGC) representations, where a regularized orthogonal forward regression (ROFR) algorithm is adopted to detect a parsimonious model with good generalization performance. The causality images for network input preserving time, frequency and location information of connectivity are then designed based on the TF-CGC distributions of alpha band multichannel EEG signals. Further constructed boosted ConvNets by using spatio-temporal convolutions as well as advances in deep learning including cropping and boosting methods, to extract discriminative causality features and classify MI tasks. Our proposed approach outperforms the competition winner algorithm with 12.15% increase in average accuracy and 74.02% decrease in associated inter subject standard deviation for the same binary classification on BCI competition-IV dataset-IIa. Experiment results indicate that the boosted ConvNets with causality images works well in decoding MI-EEG signals and provides a promising framework for developing MI-BCI systems.

Telling cause from effect in deterministic linear dynamical systems

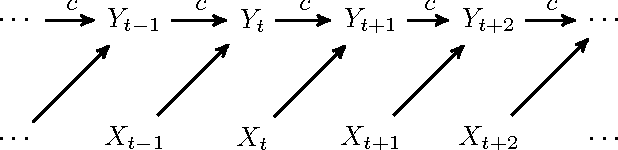
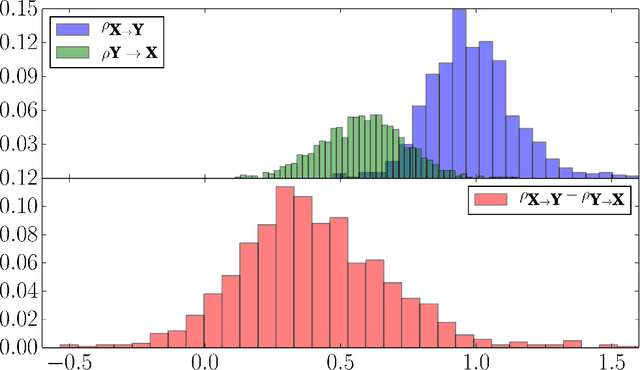
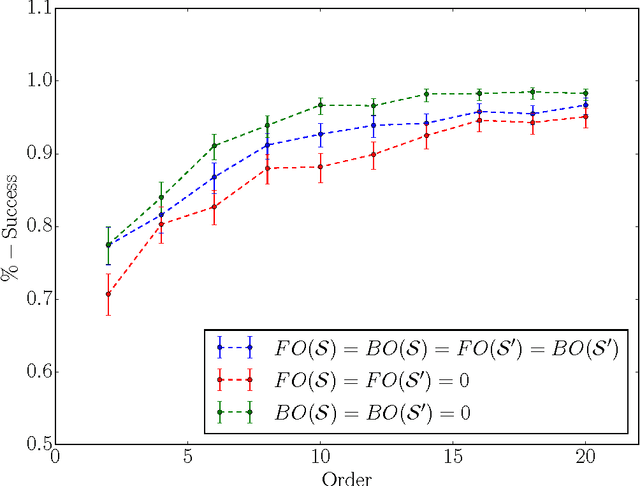
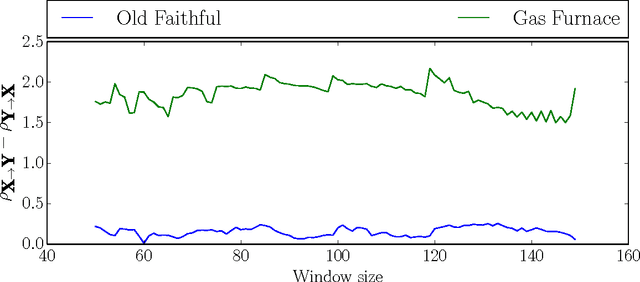
Inferring a cause from its effect using observed time series data is a major challenge in natural and social sciences. Assuming the effect is generated by the cause trough a linear system, we propose a new approach based on the hypothesis that nature chooses the "cause" and the "mechanism that generates the effect from the cause" independent of each other. We therefore postulate that the power spectrum of the time series being the cause is uncorrelated with the square of the transfer function of the linear filter generating the effect. While most causal discovery methods for time series mainly rely on the noise, our method relies on asymmetries of the power spectral density properties that can be exploited even in the context of deterministic systems. We describe mathematical assumptions in a deterministic model under which the causal direction is identifiable with this approach. We also discuss the method's performance under the additive noise model and its relationship to Granger causality. Experiments show encouraging results on synthetic as well as real-world data. Overall, this suggests that the postulate of Independence of Cause and Mechanism is a promising principle for causal inference on empirical time series.